Algorithme de Pohlig-Hellman

Si ce bandeau n'est plus pertinent, retirez-le. Cliquez ici pour en savoir plus.

Certaines informations figurant dans cet article ou cette section devraient être mieux reliées aux sources mentionnées dans les sections « Bibliographie », « Sources » ou « Liens externes » (juin 2018).

Vous pouvez améliorer la vérifiabilité en associant ces informations à des références à l'aide d'appels de notes.

L’algorithme de Pohlig-Hellman^[1] est un algorithme pour résoudre le problème du logarithme discret^[2] (PLD). Il divise un PLD en sous-problèmes (tous des PLD aussi) et utilise ensuite les résultats de ces sous-problèmes pour construire la solution.

Le problème du logarithme discret[modifier | modifier le code]

Soit $G=\langle g\rangle$ un groupe cyclique engendré par g. Soient h un élément de G, et N l'ordre de G.

On cherche x tel que g^x = h.

Si une telle solution existe, alors il en existe une dans {0, 1, … , N – 1}; on peut la trouver par exemple par une réduction modulaire.

En effet, par le Théorème de Lagrange, on a $g^{N}=1_{G}$ , ainsi si $x\equiv x'\ ({\bmod {\ }}N)$ avec $x'\in [\![0;N-1]\!]$ , alors il existe un entier relatif k ∈ ℤ tel que $x=x'+k\cdot N$ . Par conséquent : $h=g^{x}=g^{x'+k\cdot N}=g^{x'}\cdot (g^{N})^{k}=g^{x'}$ .

On peut donc considérer les solutions $x\in \mathbb {Z} /N\mathbb {Z} .$

L'algorithme[modifier | modifier le code]

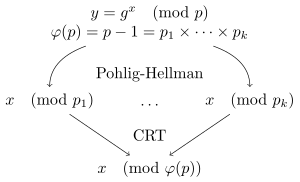
Algorithme de Pohlig-Hellman — Diagramme explicatif montrant les différentes étapes de l’algorithme. CRT signifie théorème des restes chinois (*Chinese Remainder Theorem* en anglais)

En utilisant la décomposition en produit de facteurs premiers, on peut écrire $N=\prod _{i=1}^{n}p_{i}^{u_{i}}$ .

Pour chaque i allant de 1 à n on pose :

$g_{i}=g^{N/p_{i}^{u_{i}}},\quad h_{i}=h^{N/p_{i}^{u_{i}}}$ .

Soit $x_{i}$ une solution modulo $p_{i}^{u_{i}}$ pour le PLD $g_{i}^{x_{i}}=h_{i}$ (on peut par exemple utiliser un algorithme comme baby-step giant-step ou Pollard-rho pour cette étape).

On peut alors appliquer le théorème des restes chinois pour trouver une solution $x\in \mathbb {Z} /N\mathbb {Z}$ tel que pour chaque i de 1 à n on ait

x\equiv x_{i}{\pmod {p_{i}^{u_{i}}}}

.

Le théorème des restes chinois assure que ce $x$ est bien une solution valide pour le PLD g^x = h.

Conséquences[modifier | modifier le code]

Dans la cryptanalyse du PLD, cet algorithme permet d'affirmer que la difficulté du logarithme discret dans un groupe d'ordre $N=\prod _{i=1}^{n}p_{i}^{u_{i}}$ avec $p_{1}<\ldots <p_{n}$ se ramène à la difficulté du logarithme discret dans $p_{n}^{u_{n}}$ .

Une conséquence de cette remarque est que les groupes d'ordre friable sont à éviter en cryptographie lorsque l’on souhaite utiliser l'hypothèse du logarithme discret comme hypothèse de complexité (ou toute autre hypothèse plus forte), puisqu’il suffirait de résoudre les différents logarithmes discrets dans des groupes de petites tailles, où il serait possible d'utiliser un algorithme comme l'algorithme rho de Pollard en temps raisonnable.

Notes et références[modifier | modifier le code]

↑ Pohlig et Hellman 1978.
↑ Thomé 2003.

Annexes[modifier | modifier le code]

Articles connexes[modifier | modifier le code]

Bibliographie[modifier | modifier le code]

[Menezes, van Oorschot et Vanstone 1996] (en) Alfred J. Menezes, Paul C. van Oorschot et Scott A. Vanstone, Handbook of Applied Cryptography, Boca Raton, CRC Press, 1996, 816 p. (ISBN 978-0-8493-8523-0, BNF 37515673, lire en ligne), « Section 3.6.4 : Pohlig-Hellman algorithm ».
[Pohlig et Hellman 1978] (en) Stephen C. Pohlig et Martin E. Hellman, « An Improved Algorithm for Computing Logarithms over GF(p) and its Cryptographic Significance », IEEE Transactions on Information Theory, n^o 24,‎ 1978, p. 106-110 (lire en ligne)
[Thomé 2003] Emmanuel Thomé, Algorithmes de calcul de logarithmes discrets dans les corps finis (thèse de doctorat en informatique), 2003 (lire en ligne), « Section 2.1 : L'algorithme de Pohlig-Hellman »

[PohligHellman1978-1] Pohlig et Hellman 1978.

[Thomé2003-2] Thomé 2003.

[1]

[2]