Graphe de Heawood

Graphe de Heawood
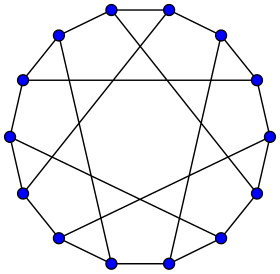Représentation du graphe de Heawood.
Nombre de sommets	14
Nombre d'arêtes	21
Distribution des degrés	3-régulier
Rayon	3
Diamètre	3
Maille	6
Automorphismes	336 (PGL(2,7))
Nombre chromatique	2
Indice chromatique	3
Propriétés	Cage Cubique Biparti Graphe de Cayley Graphe de Moore Hamiltonien Symétrique Parfait

En théorie des graphes, le graphe de Heawood est un graphe cubique symétrique possédant 14 sommets et 21 arêtes. Il doit son nom à Percy John Heawood, un mathématicien britannique né en 1861 et mort en 1955.

Propriétés

Propriétés générales

Le graphe de Heawood est une (3,6)-cage, c'est-à-dire un graphe minimal en nombres de sommets ayant une maille de 6 et étant cubique. En fait, il s'agit de l'unique (3,6)-cage et sa taille coïncide avec la borne de Moore, une borne inférieure sur le nombre de sommets que peut avoir une cage. Un tel graphe est qualifié de graphe de Moore.

Le diamètre du graphe de Heawood et son rayon sont tous deux égaux à 3. Cela entraîne que tous ses sommets appartiennent à son centre.

Le graphe de Heawood est 3-sommet-connexe et 3-arête-connexe, c'est-à-dire qu'il est connexe et que pour le rendre déconnecté il faut le priver au minimum de 3 sommets ou de 3 arêtes. Comme il est régulier de degrés 3 ce nombre est optimal. Le graphe de Heawood est donc un graphe optimalement connecté.

Il est également hamiltonien, c'est-à-dire qu'il possède un cycle passant par tous les sommets une et une seule fois.

Plongements

Le graphe de Heawood n'est pas planaire. En fait pour le dessiner sur un plan il faut nécessairement que plusieurs arêtes se croisent. Il est possible de le dessiner avec seulement 3 croisements et ce nombre est minimal. En fait, d'après Pegg et Exoo, le graphe de Heawood, avec ses 14 sommets, serait le plus petit graphe cubique nécessitant 3 croisements pour être dessiné sur le plan.

Le graphe de Heawood peut par contre être plongé sur le tore, c'est donc un graphe toroïdal.

Coloration

Le nombre chromatique du graphe de Heawood est 2. C'est-à-dire qu'il est possible de le colorer avec 2 couleurs de telle façon que deux sommets reliés par une arête soient toujours de couleurs différentes. Ce nombre est minimal.

L'indice chromatique du graphe de Heawood est 3. Il existe donc une 3-coloration des arêtes du graphe telle que deux arêtes incidentes à un même sommet soient toujours de couleurs différentes. Ce nombre est minimal.

Il est possible de compter les colorations distinctes du graphe de Heawood. Cela donne une fonction dépendant du nombre de couleurs autorisé. C'est une fonction polynomiale et le polynôme qui lui est associé est qualifié de polynôme chromatique. Ce polynôme de degré 14 admet pour racines tous les entiers positifs ou nuls strictement inférieurs à 2. Il est égal à : $z(z-1)(z^{12}-20z^{11}+190z^{10}-1140z^{9}+4845z^{8}-15476z^{7}+38340z^{6}-74587z^{5}+113433z^{4}-131700z^{3}+110794z^{2}-60524z+16161)$

Propriétés algébriques

Le graphe de Heawood est symétrique, c'est-à-dire que son groupe d'automorphismes agit transitivement sur ses arêtes, ses sommets et ses arcs. Son groupe d'automorphisme est d'ordre 336 et est isomorphe au groupe projectif linéaire PGL(2,7). C'est l'unique graphe cubique symétrique à 14 sommets d'où son nom de F014A dans le Foster Census classifiant tous les graphes cubiques symétriques.

Le polynôme caractéristique de la matrice d'adjacence du graphe de Heawood est : $(x-3)(x+3)(x^{2}-2)^{6}$. C'est le seul graphe avec ce polynôme caractéristique ce qui fait de lui un graphe déterminé de façon unique par son spectre, c'est-à-dire l'ensemble des valeurs propres de sa matrice d'adjacence.

Galerie

• 
  Il est possible de dessiner le graphe de Heawood sur le plan avec seulement 3 croisements.
• 
  L'indice chromatique du graphe de Heawood est 3.
• 
  Le nombre chromatique du graphe de Heawood est 2.