Utilisateur:Proz/Pi
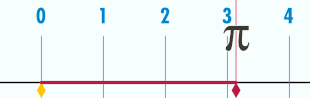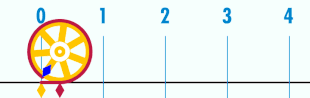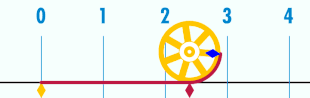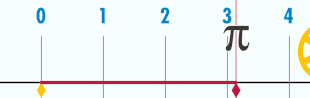
Le nombre pi, noté par la lettre grecque du même nom π (toujours en minuscule), est le rapport constant entre la circonférence d’un cercle et son diamètre dans le plan euclidien ; c'est aussi la valeur du rapport entre l'aire d'un disque et le carré de son rayon.
Le nombre π est parfois appelé constante d'Archimède. Des valeurs approchées courantes sont :
- 3,14 ; 3,1416 ; 22/7 ; 355/113[1]
Mais π est un nombre irrationnel, c’est-à-dire qu’il n’est pas le rapport de deux nombres entiers. En fait, ce nombre est transcendant. Cela signifie qu’il n'existe pas de polynôme non nul à coefficients entiers dont π soit une racine.
La transcendance de π établit l’impossibilité de résoudre le problème de la quadrature du cercle : on ne peut pas construire, à l’aide de la règle et du compas seulement, un carré dont la surface est rigoureusement égale à la surface d’un disque donné.
Définition[modifier | modifier le code]

Dans les dictionnaires et ouvrages généralistes[2], π est défini comme le rapport constant entre la circonférence d'un cercle et son diamètre (implicitement dans le plan usuel qui est le plan euclidien).
Ce rapport ne dépend pas du cercle choisi, en particulier de sa taille, car tous les cercles du plan euclidien sont semblables. Ainsi, si un cercle a le double du diamètre d d'un autre cercle, il aura aussi le double de sa circonférence C.
On démontre que π est aussi le rapport entre la superficie d'un cercle et le carré de son rayon[3] :
Il s'avère que cette définition géométrique, historiquement la première et la plus intuitive, a une alternative plus directe pour des mathématiciens souhaitant définir π en toute rigueur. Des ouvrages plus avancés[4] définissent π par l'analyse réelle à l'aide des fonctions trigonométriques, elles-mêmes introduites sans référence à la géométrie (voir plus bas).
Approche géométrique[modifier | modifier le code]
La définition usuelle de π, celle du dictionnaire, fait appel à l'intuition géométrique. C'est aussi la première définition historiquement, ce lle qui fonde les travaux mathématiques de Babylone et l'Égypte antique, jusqu'au XVIIè siècle européen.
Justification de la définition[modifier | modifier le code]
La définition même de π, liée au fait que rapport de la circonférence du cercle sur son diamètre reste constant, l'associe à une propriété des polygones réguliers.
En effet, un cercle peut être approché d'aussi prêt que possible par un polygone régulier inscrit dans ce cercle (ou bien dans lequel ce cercle est inscrit), et d'autre part, le théorème de Thalès permet de montrer que, le nombre de côtés d'un polygone régulier étant fixé, son périmètre est proportionnel au rayon du cercle dans lequel il est inscrit. Cette propriété étant vérifiée pour tout polygone régulier inscrit, aussi grand que soit le nombre de ses côtés, on en déduit la même propriété pour le cercle par passage à la limite. Par un raisonnement analogue on obtient que l'aire du disque est proportionnelle au carré de son rayon (ou de son diamètre)
Vers 300 av. J.-C., Euclide utilise essentiellement cette méthode pour démontrer ces résultats (à vérifier pour le périmètre, disque/carré prop 2 du livre XII). Ces résultats sont cependant très intuitifs , et connus et attestés depuis très longtemps[5].

Aire et périmètre[modifier | modifier le code]
De même l'aire de tout polygone régulier est égale au demi-périmètre de celui-ci multiplié par la distance du centre du polygone à un de ses côtés. En effet, par un simple découpage en triangles isocèles de sommets le centre d'un polygone régulier à nombre pair de côtés, on reconstitue un parallélogramme de hauteur cette distance et de base le demi-périmètre. Là encore cette propriété est vérifiée pour tout polygone régulier inscrit dans un cercle, quel que soit le nombre de ses côtés (avec un raisonnement analogue quand celui-ci est impair). À la limite, la distance du centre à un côté du polygone devient le rayon R du cercle, la base le demi-périmètre du cercle soit πR, le parallélogramme un rectangle d'aire πR2 qui est donc l'aire du cercle de rayon R.
Au IIIe siècle av. J.-C., Archimède a donné une démonstration rigoureuse de cette propriété qui repose sur ce principe (voir ci-dessous). Mais le résultat était connu bien avant lui des Babyloniens, qui auraient pu le découvrir de cette façon[6]. Plusieurs siècle av. J.-C., les Chinois savaient également relier l'aire du disque et sa circonférence.
Par contre il semble que les Égyptiens de l'Antiquité l'ignoraient. Aire et circonférence étaient calculées indépendamment[5].
Premiers calculs[modifier | modifier le code]
Encadrement par des polygones réguliers[modifier | modifier le code]
Le périmètre de l'hexagone régulier, constitué de 6 triangles équilatéraux, est donc de 6 fois le rayon du cercle dans lequel il est inscrit. On en déduit que le nombre π est supérieur à la moitié de 6, soit 3.
Le théorème de Pythagore permet de calcul la longueur du côté de l'hexagone exinscrit au cercle soit 12/√3 fois le rayon. Le nombre π est alors inférieur à 2√3, donc à 3,5.
Cet encadrement peut être amélioré en augmentant le nombre de côtés des polygones régulier inscrit et exinscrit au cercle. Au IIIè siècle v. J.-C. Archimède décrit une méthode itérative qui permet d'encadrer π avec la précision voulue, du moins théoriquement car en pratique les calculs sont rapidement très longs. Il part de ces deux hexagones et double le nombre des côté des polygones insrits et exinscrits à chaque étape.
(voir plus bas ou article détaillé ?)
Plus de mille ans auparavant, s'ils ne donnaient pas un tel encadement, les Babyloniens utilisaient fréquemment 3 comme approximation de π dans leur tablettes d'argile[5], aussi bien pour calculer la circonférence du cercle que son aire, puisqu'ils obtiennent cette dernière en multipliant la demi-circonférence par le rayon. On trouve également dans la Bible, une indication que 3 aurait pu être utilisé, à l'époque de Salomon, pour calculer l'aire (ou la circ.je vérifie et reformule) du disque [5].
DESSIN (à trouver ou que je peux faire)
Une approximation du disque par un octogone[modifier | modifier le code]

On peut essayer de recouvrir le disque par un octogone comme dans le dessin indiqué ci-contre. À la différence de l'approximation précédente, c'est l'aire du disque que l'on cherche à approcher. Il ne s'agit pas non plus d'un encadrement : par endroit c'est le cercle qui déborde légèrement et par endroit l'octogone.
Le diamètre d est divisé par 3, l'aire du grand carré est d2, chacun des petits carrés a donc une aire de 1⁄9d2. Pour l'octogone, on retire 4 demi-carrés, soit un aire de (1 - 2⁄9)d2 (soit 63⁄81d2). On peut remarquer que l'octogone déborde un peu plus du cercle que l'inverse. Par ailleurs on peut souhaiter que l'aire du cercle soit celle d'un carré. En ajoutant à l'aire de l'octogone (1⁄9d)2, on obtient que l'aire du disque est (1 - 1⁄9)2d2 (soit 64⁄81d2). La première approximation donne :
- π ≈ 4×63⁄81≈ 3.11
La seconde donne :
- π ≈ 4×64⁄81≈ 3.16
Les Égyptiens utilisent la seconde approximation, plus précisément ils calculent l'aire du disque en enlevant 1⁄9 au diamètre, puis en élevant au carré. Il s'agit d'un exemple très ancien de tentative quadrature du cercle : étant donné un disque, trouver un carré dont l'aire est la même.
Plusieurs des problèmes du papyrus Rhind utilisent cette méthode. Un autre problème présente, sans explications, le dessin de l'octogone ci-contre (sans le cercle intérieur). Les historiens en déduisent que les Égyptiens auraient pu découvrir cette approximation comme indiqué ci-dessus[5].
La méthode d'Archimède[modifier | modifier le code]
A développer ici ou article séparé ?
Histoire : des Babyloniens à François Viète[modifier | modifier le code]
[Développement un plus sérieux historiquement des babyloniens à Viète,cf article actuel, on y parle par exemple de méthode d'exhaustion pour les dém. d'Euclide et d'Archimède]
Approche analytique [fais-en ce que tu veux][modifier | modifier le code]
Aperçu[modifier | modifier le code]
On peut reprocher à l'approche géométrique de trop reposer sur le dessin. Pour définir $\pi$ de manière plus rigoureuse, on va le définir comme le premier zéro strictement positif de la fonction sinus [je suppose ici qu'on en aurait déjà parlé], qu'il faut alors définir proprement. Pour se faire on à en gros [je sais ca ne veut rien dire, c'est pas sourcé et tout et tout mais c'est du brouillon] deux manières de faire :
- ou bien à travers la série entière qui converge, par exemple par comparaison à la série exponentielle. Une étude de cette fonction permettrait de montrer l'éxistence d'un premier zéro strictement positif.
- ou bien à travers l'exponentielle complexe . Quelques arguments topologiques permettraient alors de conclure.
- ou bien partir de la théorie développé par Leborgne (calcul différentiel complexe, QJS, 1991) qui définit π par l'intégrale curviligne de 1/(u-z): il existe un unique nombre π>0 tel que, pour tout pavé P et tout z n'appartenant pas à la frontière de P, on ait
si z est dans l'intérieur de P, 0 sinon.
Quelques détails[modifier | modifier le code]
La complétude de montre [éventuellement renvoyer ca vers une page sur les complexes, sauf si on le fait là aussi...] que l'application prolonge l'exponentielle réelle à tout entier et vérifie les propriétés suivantes :
- ,
- .
- est une série entière partout convergente donc a fortiori continue et dérivable.
Le premier point motive la notation en puissance : déjà adoptée pour les réels. On tire du second point que pour tout réel , . On introduit alors l'application qui est un morphisme de groupes topologiques. Le but est alors de montrer qu'elle induit un isomorphisme de sur et d'en déduire qu'il existe un unique réel positif, noté , tel que .
Voici quelques arguments topologiques pour trancher, on propose juste après une approche plus trigonométrique. Comme est non triviale (on peut voir que la partie imaginaire de est strictement positive), son image est un sous-groupe non-trivial connexe de ce qui permet d'obtenir la surjectivité. Son noyau doit alors être fermé et comme est compact, il est non trivial (et pas non-plus égal à ), du coup il est de la forme pour un unique réel . On pose .
Trigonométrie[modifier | modifier le code]
On définit ici les fonctions cosinus et sinus sur comme étant respectivement les parties réelle et imaginaire de . Ainsi par définition est le seul couple réel vérifiant . Il s'en suit que :
et on en déduit également les formules d'Euler : et
qui prouvent que ce sont des fonctions dérivables. En dérivant la définition on obtient et par unicité de l'écriture algébrique il vient :
- et .
On montre alors, par l'absurde, que cosinus s'annule. Sinon, comme elle est continue et positive en elle serait toujours strictement positive par le TVI, et par suite serait strictement croisssante : donnsons nous a>0 tel que . Alors on a pour tout x>a :
qui tend vers quand et donc aussi, ce qui est la contradiction voulue. Bref est non vide. On pose alors . Par continuité de on a et est le plus petit réel strictement positif à vérifier cette relation. On a maintenant et d'où découle
et donc et . Puisque on a la très jolie formule : . On a aussi ce qui donne la -périodicité de et donc de et . [A ce stade je verrais bien un petit tableau récapitulatif et les graphes des fonctions.] On peut maintenant prouver que induit un isomorphisme entre et .
On sait déjà que . Réciproquement si s'écrit algébriquement alors et donc et par théorème des valeurs intermédiaires il existe tel que . Par suite et quitte à changer en , ce qui ne change rien à , on peut supposer que . Bref, et est bien surjective sur . Enfin pour tout d'après l'étude menée précédemment.
Vérifications[modifier | modifier le code]
Il nous faut maintenant vérifier que défini ainsi, n'en reste pas moins le rapport périmètre/diamètre ou de façon équivalente l'aire d'un cercle de rayon 1. Pour ce faire on peut calculer l'aire d'un quart de cerle de rayon 1, ie l'aire sous la courbe . Il vient
.
Si l'équivalence géométrique ne nous convient pas, le calcul intégral permet également de montrer que la longueur, disons d'un demi-cercle de rayon 1, vaut bien .
Quelques propriétés mathématiques de [modifier | modifier le code]
Nature de [modifier | modifier le code]
Le fait que soit le premier zéro de sinus conduit à une preuve élémentaire de son irrationnailité, ie qu'on ne peut le mettre sous une forme de fraction a/b avec a et b entiers. Pour le voir on procède par l'absurde et on considère par exemple (une autre preuve sera fournie dans la partie Histoire) intégrales suivantes . Elles sont toutes strictement positives justement parceque l'intégrande est positif, continue et non identiquement nul. Par contre on peut majorer x(a-bx) sur disons par M et donc tend vers 0 avec n. Enfin, on montre en intégrant 2n+1 fois par parties, que est un entier ce qui amène la contradiction.
Ainsi n'est pas rationnel, a fortiori non décimal et ne présente même pas un developpement décimal périodique. En connaître toujours plus de décimales deviendra un défi pour les mathématiciens et les informaticiens (cf l'endroit qui en reparlera). Plus difficilement, on peut montrer que est transcendant, ie n'annule aucun polynome non nul à coefficient entier. [plus de détails ici ou dans la partie historique ?]
[lambert. les fractions continues.]
Quelques formules remarquables[modifier | modifier le code]
[j'en suis pas fan du tout et ca me parait tres arbitraire, mais j'y berrais quand même] stirling, intégrale gaussienne, formule des résidus
Quelques questions ouvertes[modifier | modifier le code]
On ne sait pas si e et pi sont algébriquement indépendants... (après j'en sais rien, peut-être des question sur la répartition des décimales ?)
Il y en a quelques unes sur ce lien, par exemple dzeta de 3 divisé par Pi au cube est-il un rationnel (cf ce qui passe avec la fonction zêta de Riemann calculée sur les entiers pairs.
Approche de [modifier | modifier le code]
Tout d'abord, il faut comprendre qu'on ne peut donner de valeur décimale exacte de $\pi$. En fait on peut montrer que $\pi$ est irrationnel, et même beaucoup plus difficilement transcendant, ie que $\pi$ n'annule aucun polynôme à coefficients rationnels. Ce dernier résultat fut montré pour la première fois par Lindemann en 1882 ce qui prouvait au passage l'impossibilité de la quadrature du cercle [Oula j'ai un doute sur l'antériorité les travaux de Wantzel sur la constructibilité...(moi pas !)]. Si, pour des raisons pratiques, il est indispensable de disposer des premières décimales de $\pi$, le calcul d'un nombre toujours plus grand de décimales exactes à motiver de nombreux travaux. [je m'arrete là parce que je n'y connais vraiment rien là !]
Voir aussi[modifier | modifier le code]
Notes et références[modifier | modifier le code]
- Gourdon, Xavier; Pascal Sebah. "Collection of approximations for π". Numbers, constants and computation. http://numbers.computation.free.fr/Constants/Pi/piApprox.html. Retrieved 2007-11-08.
- Par exemple le Petit Robert ou le [tlfi ttp://atilf.atilf.fr]
- (en) Bettina Richmond, « Area of a Circle », Western Kentucky University, (consulté le )
- Par exemple J.Lelong-Ferrand, J.M. Arnaudiès, cours de mathématiques Tome 2, Dunod Université, 4e édition 1977
- (en) Victor J. Katz, History of Mathematics: An Introduction, Addison–Wesley, , 2e éd. (ISBN 0321016181, OCLC 38199387 60154481) p 20
- Katz, même ouvrage, p 22


























































![{\displaystyle x\in [-1,1]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/1f9d0dda56ce3e01e14570ac9aef0021c6125722)









![{\displaystyle \int _{0}^{1}{\sqrt {1-x^{2}}}dx=\int _{0}^{\frac {\pi }{2}}\sin ^{2}\theta d\theta =\int _{0}^{\frac {\pi }{2}}{\frac {1-\cos 2\theta }{2}}d\theta ={\frac {\pi }{4}}-\left[{\frac {\sin 2\theta }{4}}\right]_{0}^{\frac {\pi }{2}}={\frac {\pi }{4}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/fb563e3d0da245bd689fda8b0f8039227b0ed158)

![{\displaystyle [0,\pi ]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/3e2a912eda6ef1afe46a81b518fe9da64a832751)

